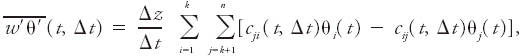Nonlocal flux: Difference between revisions
From Glossary of Meteorology
No edit summary |
m (Rewrite with Template:Term and clean up) |
||
| Line 1: | Line 1: | ||
{{Term | |||
|Display title=nonlocal flux | |||
{{ | |Definitions={{Definition | ||
|Num=1 | |||
|Meaning=The vertical [[turbulent transport]] of a quantity such as [[heat]] per unit area per time across any height index ''k'', between [[source]] heights ''j'' to destination heights ''i'', where ''i'' and ''j'' are on opposite sides of ''k'' vertically. | |||
|Explanation=It is nonlocal because ''i'' and ''j'' need not be neighbors. Using kinematic [[heat flux]] as an example, <blockquote>[[File:ams2001glos-Ne7.gif|link=|center|ams2001glos-Ne7]]</blockquote> where ''n'' is the total number of [[grid]] cells in a vertical column, Δ''z'' is the vertical thickness of each grid cell (i.e., spacing between grid points), Δ''t'' is the time increment over which [[eddies]] transport heat starting from time ''t'', θ<sub>''a''</sub> is the [[potential temperature]] at grid cell ''a'', and ''c''<sub>''ab''</sub> is the [[transilient matrix|transilient matrix]] specifying the fraction of air that ended in destination cell ''a'' originated at source cell ''b'', for ''a'' and ''b'' dummy indices. <br/>''See'' [[transilient turbulence theory]], [[nonlocal mixing]]. | |||
}} | |||
= | }} | ||
Latest revision as of 09:29, 27 March 2024
The vertical turbulent transport of a quantity such as heat per unit area per time across any height index k, between source heights j to destination heights i, where i and j are on opposite sides of k vertically.
It is nonlocal because i and j need not be neighbors. Using kinematic heat flux as an example,
See transilient turbulence theory, nonlocal mixing.
where n is the total number of grid cells in a vertical column, Δz is the vertical thickness of each grid cell (i.e., spacing between grid points), Δt is the time increment over which eddies transport heat starting from time t, θa is the potential temperature at grid cell a, and cab is the transilient matrix specifying the fraction of air that ended in destination cell a originated at source cell b, for a and b dummy indices.
See transilient turbulence theory, nonlocal mixing.