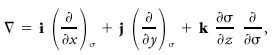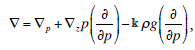Del operator: Difference between revisions
(Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == del operator == </div> <div class="definition"><div class="short_definition">The [[operator...") |
m (Rewrite with Template:Term and clean up) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== del operator == | == del operator == | ||
The [[operator]] (written '''∇''') is used to transform a [[scalar]] field into the [[ascendent]] (the negative of the [[gradient]]) of that [[field]].<br/> In [[Cartesian coordinates]] the three-dimensional del operator is <blockquote>[[File:ams2001glos-De16.gif|link=|center|ams2001glos-De16]]</blockquote> and the horizontal component is <blockquote>[[File:ams2001glos-De17.gif|link=|center|ams2001glos-De17]]</blockquote> Expressions for '''∇''' in various systems of [[curvilinear coordinates]] may be found in any textbook of [[vector]] analysis. In meteorology it is often convenient to use a [[thermodynamic function of state|thermodynamic function of state]], such as [[pressure]] or [[potential temperature]], as the vertical coordinate. If the chosen function is ''σ'', then <blockquote>[[File:ams2001glos-De18.gif|link=|center|ams2001glos-De18]]</blockquote> where differentiation with respect to ''x'' and ''y'' is understood as carried out on surfaces of constant ''σ'' (the subscript usually being omitted). The horizontal component is now <blockquote>[[File:ams2001glos-De19.gif|link=|center|ams2001glos-De19]]</blockquote> If the [[quasi-hydrostatic approximation]] is justified, as in most meteorological contexts, pressure is a useful coordinate, and <blockquote>[[File:ams2001glos-De20_revised2.gif|link=|center|ams2001glos-De20_revised2]]</blockquote> where ''g'' is the [[acceleration of gravity]] and ''ρ'' is the [[density]]. Here <blockquote>[[File:ams2001glos-De21.gif|link=|center|ams2001glos-De21]]</blockquote> with differentiation carried out in [[isobaric surfaces]], and '''∇'''<sub>''z''</sub> is the horizontal gradient operator in Cartesian-altitude coordinates.<br/> | |||
<p>''Term updated 8 March 2017.''</p> | |||
Latest revision as of 12:04, 27 March 2024
del operator
The operator (written ∇) is used to transform a scalar field into the ascendent (the negative of the gradient) of that field.
In Cartesian coordinates the three-dimensional del operator is
and the horizontal component is
Expressions for ∇ in various systems of curvilinear coordinates may be found in any textbook of vector analysis. In meteorology it is often convenient to use a thermodynamic function of state, such as pressure or potential temperature, as the vertical coordinate. If the chosen function is σ, then
where differentiation with respect to x and y is understood as carried out on surfaces of constant σ (the subscript usually being omitted). The horizontal component is now
If the quasi-hydrostatic approximation is justified, as in most meteorological contexts, pressure is a useful coordinate, and
where g is the acceleration of gravity and ρ is the density. Here
with differentiation carried out in isobaric surfaces, and ∇z is the horizontal gradient operator in Cartesian-altitude coordinates.
Term updated 8 March 2017.