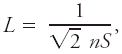Mean free path: Difference between revisions
From Glossary of Meteorology
(Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == mean free path == </div> #<div class="definition"><div class="short_definition">Average dis...") |
m (Rewrite with Template:Term and clean up) |
||
| Line 1: | Line 1: | ||
{{Term | |||
|Display title=mean free path | |||
{{ | |Definitions={{Definition | ||
|Num=1 | |||
|Meaning=#Average distance a molecule travels in a gas between collisions. | |||
|Explanation=This concept has a meaning only to the extent that the paths of molecules are mostly straight lines interrupted by changes in direction (collisions) over comparatively shorter distances of order the molecular size. Molecules in a liquid are never free in this sense. The mean free path ''L'' in a gas of a single molecular species with a [[Maxwell–Boltzmann distribution]] of speeds is <blockquote>[[File:ams2001glos-Me7.gif|link=|center|ams2001glos-Me7]]</blockquote> where ''n'' is the number [[density]] of molecules and ''S'' is the mutual collision [[cross section]]. To the extent that a molecule can be considered a hard sphere with diameter ''d'', ''S'' = π''d''<sup>2</sup>. The concept of molecular diameter is fuzzy and each method for determining it yields different results (Kennard 1938). At [[sea level]] the mean free path in air is of order 0.1 μm.<br/> | |||
#Average distance a [[photon]] travels in a turbid medium between [[scattering]] (scattering mean free path) events, or the average distance a photon travels before being absorbed ([[absorption]] mean free path).<br/> The scattering mean free path in a medium is the inverse of its [[scattering coefficient]]; the absorption mean free path is the inverse [[absorption coefficient]]; and the total mean free path is the inverse of the sum of scattering and absorption coefficients. At visible wavelengths, the scattering mean free path in clouds is of order 10 m.<br/> Kennard, E. H. 1938. Kinetic Theory of Gases. 97–114. | |||
}} | |||
}} | |||
# | |||
# | |||
Latest revision as of 10:46, 29 March 2024
- Average distance a molecule travels in a gas between collisions.
where n is the number density of molecules and S is the mutual collision cross section. To the extent that a molecule can be considered a hard sphere with diameter d, S = πd2. The concept of molecular diameter is fuzzy and each method for determining it yields different results (Kennard 1938). At sea level the mean free path in air is of order 0.1 μm.
- Average distance a photon travels in a turbid medium between scattering (scattering mean free path) events, or the average distance a photon travels before being absorbed (absorption mean free path).
The scattering mean free path in a medium is the inverse of its scattering coefficient; the absorption mean free path is the inverse absorption coefficient; and the total mean free path is the inverse of the sum of scattering and absorption coefficients. At visible wavelengths, the scattering mean free path in clouds is of order 10 m.
Kennard, E. H. 1938. Kinetic Theory of Gases. 97–114.