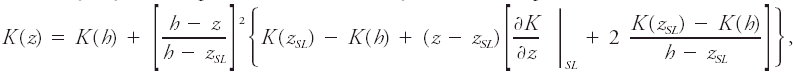O'brien cubic polynomial: Difference between revisions
From Glossary of Meteorology
No edit summary |
m (Rewrite with Template:Term and clean up) |
||
| Line 1: | Line 1: | ||
{{Term | |||
|Display title=O'Brien cubic polynomial | |||
{{ | |Definitions={{Definition | ||
|Num=1 | |||
|Meaning= | |||
An approximation for the [[eddy diffusivity]] ''K'' as a function of height ''z'' in a [[boundary layer]] of depth ''h'' with [[surface layer]] (SL) of depth ''z''<sub>''SL''</sub>: <blockquote>[[File:ams2001glos-Oe1.gif|link=|center|ams2001glos-Oe1]]</blockquote> where the tunable parameters in the equation are eddy diffusivities at the top of the surface layer and at the top of the boundary layer, ''K''(''z''<sub>''SL''</sub>) and ''K''(''h''), respectively, the heights of those two layers, and the [[gradient]] of eddy diffusivity at the top of the surface layer ∂''K''/∂''z''.<br/> Above the top of the boundary layer the eddy diffusivity is assumed to be constant at ''K''(''h''), while at the surface it is assumed to be zero. <br/>''See'' [[K-theory]], [[gradient transport theory]], [[first-order closure|first-order closure]], [[closure assumptions]].<br/> O'Brien, J. J. 1970. A note on the vertical structure of the eddy exchange coefficient in the planetary boundary layer. J. Atmos. Sci.. 27. 1213–1215. | |||
}} | |||
}} | |||
Latest revision as of 03:20, 27 March 2024
An approximation for the eddy diffusivity K as a function of height z in a boundary layer of depth h with surface layer (SL) of depth zSL:
Above the top of the boundary layer the eddy diffusivity is assumed to be constant at K(h), while at the surface it is assumed to be zero.
See K-theory, gradient transport theory, first-order closure, closure assumptions.
O'Brien, J. J. 1970. A note on the vertical structure of the eddy exchange coefficient in the planetary boundary layer. J. Atmos. Sci.. 27. 1213–1215.
where the tunable parameters in the equation are eddy diffusivities at the top of the surface layer and at the top of the boundary layer, K(zSL) and K(h), respectively, the heights of those two layers, and the gradient of eddy diffusivity at the top of the surface layer ∂K/∂z.
Above the top of the boundary layer the eddy diffusivity is assumed to be constant at K(h), while at the surface it is assumed to be zero.
See K-theory, gradient transport theory, first-order closure, closure assumptions.
O'Brien, J. J. 1970. A note on the vertical structure of the eddy exchange coefficient in the planetary boundary layer. J. Atmos. Sci.. 27. 1213–1215.