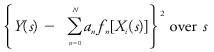Least squares: Difference between revisions
From Glossary of Meteorology
No edit summary |
m (Rewrite with Template:Term and clean up) |
||
| Line 1: | Line 1: | ||
{{Term | |||
|Display title=least squares | |||
{{ | |Definitions={{Definition | ||
|Num=1 | |||
|Meaning=Any procedure that involves minimizing the sum of squared differences. | |||
|Explanation=For example, the [[deviation]] of the mean from the [[population]] is less, in the square sense, than any other [[linear]] combination of the population values. This procedure is most widely used to obtain the constants of a representation of a known [[variable]] ''Y'' in terms of others ''X''<sub>''i''</sub>. Let ''Y''(''s'') be represented by <blockquote>[[File:ams2001glos-Le11.gif|link=|center|ams2001glos-Le11]]</blockquote> The ''a''<sub>''n''</sub>'s are the constants to be determined, the ''f''<sub>''n''</sub>'s are arbitrary functions, and ''s'' is a [[parameter]] common to ''Y'' and ''X''<sub>''i''</sub>. ''N'' is usually far less than the number of known values of ''Y'' and ''X''<sub>''i''</sub>. The system of equations being overdetermined, the constants ''a''<sub>''n''</sub> must be "fitted." The least squares determination of this "fit" proceeds by summing, or integrating when ''Y'' and ''X''<sub>''i''</sub> are known continuously, <blockquote>[[File:ams2001glos-Le12.gif|link=|center|ams2001glos-Le12]]</blockquote> and minimizing the sum with respect to the ''a''<sub>''n''</sub>'s. In particular, for example, if ''f''<sub>''n''</sub>[''X''<sub>''i''</sub>(''s'')] ≡ ''X''<sub>''i''</sub>(''s''), then the [[regression function]] is being determined; and when ''f''<sub>''n''</sub>[''X''<sub>''i''</sub>(''s'')] ≡ cos ''n''''X''<sub>''i''</sub>(''s''), or sin ''n''''X''<sub>''i''</sub>(''s''), then ''Y'' is being represented by a multidimensional [[Fourier series]]. Least squares is feasible only when the unknown constants ''a''<sub>''n''</sub> enter linearly. The [[method of least squares]] was described independently by Legendre in 1806, Gauss in 1809, and Laplace in 1812. | |||
}} | |||
= | }} | ||
Latest revision as of 05:33, 29 March 2024
Any procedure that involves minimizing the sum of squared differences.
For example, the deviation of the mean from the population is less, in the square sense, than any other linear combination of the population values. This procedure is most widely used to obtain the constants of a representation of a known variable Y in terms of others Xi. Let Y(s) be represented by
The an's are the constants to be determined, the fn's are arbitrary functions, and s is a parameter common to Y and Xi. N is usually far less than the number of known values of Y and Xi. The system of equations being overdetermined, the constants an must be "fitted." The least squares determination of this "fit" proceeds by summing, or integrating when Y and Xi are known continuously,
and minimizing the sum with respect to the an's. In particular, for example, if fn[Xi(s)] ≡ Xi(s), then the regression function is being determined; and when fn[Xi(s)] ≡ cos n'Xi(s), or sin n'Xi(s), then Y is being represented by a multidimensional Fourier series. Least squares is feasible only when the unknown constants an enter linearly. The method of least squares was described independently by Legendre in 1806, Gauss in 1809, and Laplace in 1812.