balance equation
From Glossary of Meteorology
In general, an equation expressing a balance of quantities in the sense that the local or individual rates of change are zero.
More specifically, it is a diagnostic equation expressing a balance between the pressure field and the horizontal field of motion: 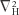 the corresponding Laplacian operator, g the acceleration of gravity, z the elevation of the isobaric surface, and subscripts denote partial differentiation. The balance equation is derived from the divergence equation on the assumption that the magnitude of the horizontal divergence is always much less than that of the (vertical) vorticity, and is therefore more general than the equation of geostrophic equilibrium to which it reduces in the absence of the nonlinear terms. In the case of circular contours, this nonlinear correction is the same as that introduced by the gradient wind assumption.
the corresponding Laplacian operator, g the acceleration of gravity, z the elevation of the isobaric surface, and subscripts denote partial differentiation. The balance equation is derived from the divergence equation on the assumption that the magnitude of the horizontal divergence is always much less than that of the (vertical) vorticity, and is therefore more general than the equation of geostrophic equilibrium to which it reduces in the absence of the nonlinear terms. In the case of circular contours, this nonlinear correction is the same as that introduced by the gradient wind assumption.
where ψ is the streamfunction for the nondivergent portion of the motion, f the Coriolis parameter, ∇H the horizontal del operator in the isobaric surface,
