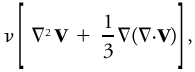The force per unit volume or per unit mass arising from the action of tangential stresses in a moving viscous fluid; this force may then be introduced as a term in the equations of motion.
By far the most satisfactory hypothesis to date is that of Navier and Stokes, a generalization of the Newtonian friction law, which evaluates the stress tensor as directly proportional to the rate of deformation, the constant of proportionality being the dynamic viscosity. In this case, the viscous force per unit mass becomes
See Navier–Stokes equations.
Townsend, A. A. 1956. The Structure of Turbulent Shear Flow. Cambridge University Press, . p. 30.
By far the most satisfactory hypothesis to date is that of Navier and Stokes, a generalization of the Newtonian friction law, which evaluates the stress tensor as directly proportional to the rate of deformation, the constant of proportionality being the dynamic viscosity. In this case, the viscous force per unit mass becomes
where ν is the kinematic viscosity, V the velocity vector, and ∇ the del operator. The divergence term, ∇·V, vanishes for an incompressible fluid, and the Navier–Stokes assumption is seen as leading to a simple diffusion of momentum. "It may seem a little strange that viscosity, which is a diffusion of momentum, can also diffuse energy and even Reynolds stresses. . . . A viscous stress acts both to convert mechanical energy into heat and to accelerate neighboring fluid, and this acceleration is an energy transfer. . . ." (Townsend 1956).
See Navier–Stokes equations.
Townsend, A. A. 1956. The Structure of Turbulent Shear Flow. Cambridge University Press, . p. 30.