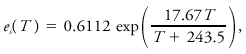Clausius-Clapeyron equation

(Also called Clapeyron equation, Clapeyron–Clausius equation.) The differential equation relating pressure of a substance to temperature in a system in which two phases of the substance are in equilibrium.
Two general expressions are

where p is the pressure, T the temperature, δs the difference in specific entropy between the phases, δv the difference in specific volume between the two phases, and L the latent heat of the phase change. The form most familiar in meteorology, related to the phase change between water vapor and liquid water, is obtained after some approximations as

where e_s is the saturation vapor pressure of water, L_v the latent heat of vaporization, and R_v the gas constant for water vapor. A similar relation for the saturation vapor pressure in contact with an ice surface is obtained by replacing the latent heat of vaporization by that of sublimation. These equations may be integrated to obtain explicit relationships between e_s and T, given known values at some point. The most empirically accurate relationships differ slightly from results so obtained. An expression believed accurate to 0.3% for -35°C < T < 35°C is given by Bolton as

where T is temperature in °C and vapor pressure is in kPa.
Iribarne, J. V., and W. L. Godson. 1981. Atmospheric Thermodynamics. D. Reidel, p. 65.
Bolton, D. 1980. The computation of equivalent potential temperature. Mon. Wea. Rev., 108. 1046–1053.

Ecuación de Clausius-Clapeyron

(También es conocida como ecuación de Clapeyron o ecuación de Clapeyron-Clausius). Es una ecuación diferencial que relaciona la presión de una sustancia con la temperatura en un sistema en el que dos fases de la sustancia están en equilibrio.

Dos expresiones generales son

donde p es la presión, T la temperatura, δs es la diferencia de entropía específica entre las fases, δv es la diferencia de volumen específico entre las dos fases y L es el calor latente del cambio de fase. La forma que se usa más en meteorología, que se relaciona con el cambio de fase entre vapor de agua y agua líquida, se obtiene después de algunas aproximaciones,

donde es es la presión de saturación del vapor del agua, L_v es el calor latente de evaporación y R_v es la constante de los gases para el vapor de agua. Se puede obtener una relación similar para la presión de saturación del vapor en contacto con una superficie de hielo al sustituir el calor latente de evaporación por el de sublimación. Se pueden integrar estas ecuaciones para obtener relaciones explícitas entre e_s y T, considerando valores conocidos en algún momento. Las relaciones empíricamente más precisas difieren ligeramente de los resultados obtenidos de esta manera. Bolton proporciona una expresión que se considera precisa al 0.3 % para -35 °C < T < 35 °C

donde T es la temperatura en °C y la presión de vapor se expresa en kPa.

Term edited 1 June 2022.

1. A type of stress characterized by uniformity in all directions.

(Or phase transformation.) A thermodynamic process in which a substance changes from one phase to another.

A collection of ideas and axioms, leading to differential equations specifying rates of change, that describes our experience with processes that involve fluxes of heat and changes in energy content.