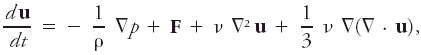Navier–Stokes equations
From Glossary of Meteorology
The equations of motion for a viscous fluid that may be written
For an incompressible fluid, the term in ∇ · u (divergence) vanishes and the effects of viscosity then play a role analogous to that of temperature in thermal conduction and to that of density in simple diffusion. Solutions of the Navier–Stokes equations have been obtained only in a limited number of special cases; in atmospheric motion, the effects of molecular viscosity are usually overshadowed by the action of turbulent processes and the Navier–Stokes equations have been of little direct application. The use of the concept of eddy viscosity has overcome this limitation in certain problems. The equations are derived on the basis of certain simplifying assumptions concerning the stress tensor of the fluid; in one dimension they represent the assumption referred to as the Newtonian friction law.
See also Ekman spiral, logarithmic velocity profile.
where p is the pressure, ρ the density, F the total external force, u the fluid velocity, and ν the kinematic viscosity.
For an incompressible fluid, the term in ∇ · u (divergence) vanishes and the effects of viscosity then play a role analogous to that of temperature in thermal conduction and to that of density in simple diffusion. Solutions of the Navier–Stokes equations have been obtained only in a limited number of special cases; in atmospheric motion, the effects of molecular viscosity are usually overshadowed by the action of turbulent processes and the Navier–Stokes equations have been of little direct application. The use of the concept of eddy viscosity has overcome this limitation in certain problems. The equations are derived on the basis of certain simplifying assumptions concerning the stress tensor of the fluid; in one dimension they represent the assumption referred to as the Newtonian friction law.
See also Ekman spiral, logarithmic velocity profile.