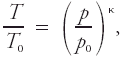Poisson equation
From Glossary of Meteorology
- The partial differential equation
where ∇2 is the Laplacian operator, φ a scalar function of position, and F a given function of the independent space variables.
For the special case F = 0, the Poisson equation reduces to the Laplace equation.
See relaxation method. - The relationship between temperature T and pressure p of an ideal gas undergoing an adiabatic process; given by
where T0 and p0 are initial state values and κ is the Poisson constant. With p0 given as a reference pressure of 100 kPa, T0 is equal to the potential temperature.